Equações Trigonométricas

INTRODUÇÃO

         Quando encontramos função trigonométrica da incógnita ou função trigonométrica de alguma função da incógnita em pelo menos um dos membros de uma equação, dizemos que esta equação é trigonométrica.

Exemplos:
1) sen x + cos x =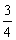  e sen 2x = cos² x  são equações trigonométricas.

2) x + ( tg 30º) . x²  e x + sen 60º = 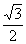 não são equações trigonométricas.

        Dizemos que r é uma raiz ou solução da equação trigonométrica f(x) = g(x) se r for elemento do domínio de f e g e se f(r) = g(r) for verdadeira.

        Na equação sen x - sen =0, por exemplo, os números  são algumas de suas raízes e os números   não o são.

        O conjunto S de todas as raízes da equação é o seu conjunto solução ou conjunto verdade.

        Quase todas as equações trigonométricas, quando convenientemente tratadas e transformadas, podem ser reduzidas a pelo menos uma das três equações seguintes:

sen x = sen a

cos x = cos a

tg x = tg a

       Estas são as equações trigonométricas elementares ou equações trigonométricas fundamentais.

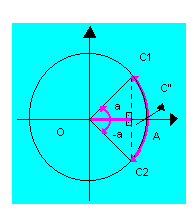
RESOLUÇÃO DA 1ª EQUAÇÃO FUNDAMENTAL

     Ela baseia-se no fato de que, se dois arcos têm o mesmo seno, então eles são côngruos ou suplementares.

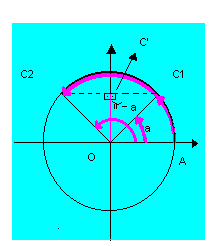
Logo, podemos escrever que:

sen x = sen a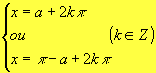

O conjunto solução dessa equação será, portanto:

         

Logo, podemos escrever que:

cos x = cos a  x = a +

O conjunto solução dessa equação será, portanto:

RESOLUÇÃO DA 3ª EQUAÇÃO FUNDAMENTAL

           Ela baseia-se no fato de que, se dois arcos têm a mesma tangente, então eles são côngruos ou têm suas  extremidades simétricas em relação  ao centro do ciclo trigonométrico.

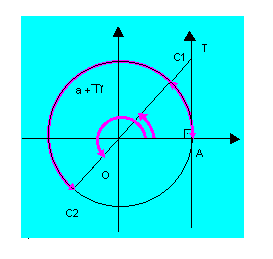
Logo, podemos escrever que:

O conjunto solução dessa equação será, portanto: